[브루트포스#4] 백준 2231번: 분해합 JAVA
2231번: 분해합
어떤 자연수 N이 있을 때, 그 자연수 N의 분해합은 N과 N을 이루는 각 자리수의 합을 의미한다. 어떤 자연수 M의 분해합이 N인 경우, M을 N의 생성자라 한다. 예를 들어, 245의 분해합은 256(=245+2+4+5)이
www.acmicpc.net
문제
어떤 자연수 N이 있을 때, 그 자연수 N의 분해합은 N과 N을 이루는 각 자리수의 합을 의미한다. 어떤 자연수 M의 분해합이 N인 경우, M을 N의 생성자라 한다. 예를 들어, 245의 분해합은 256(=245+2+4+5)이 된다. 따라서 245는 256의 생성자가 된다. 물론, 어떤 자연수의 경우에는 생성자가 없을 수도 있다. 반대로, 생성자가 여러 개인 자연수도 있을 수 있다.
자연수 N이 주어졌을 때, N의 가장 작은 생성자를 구해내는 프로그램을 작성하시오.
입력
첫째 줄에 자연수 N(1 ≤ N ≤ 1,000,000)이 주어진다.
출력
첫째 줄에 답을 출력한다. 생성자가 없는 경우에는 0을 출력한다.
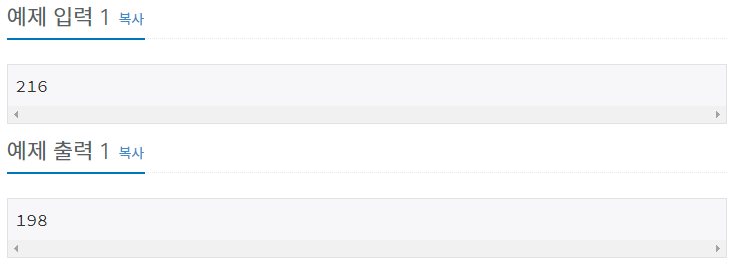
예제입출력
풀이
[브루트포스#2] 백준 4673번: 셀프 넘버 JAVA (tistory.com)
이번 문제는 위 링크의 문제와 어찌보면 같은 문제라고 할 수있다. 따라서 알고리즘을 구성하는데는 문제가 없었는데, 계속 시간초과 판정이 났다. 그래서 나름대로 시간 초과할만한 요소를 줄여보겠다고 방문여부도 체크했지만, 여전히 계속 시간초과 판정이 났다.
내가 놓치는 부분이 있었다. 문제에서 요구사항이 생성자의 최솟값을 구하는 것이였는데, 나는 1부터 검사를 해도 n의 생성자의 최솟값이 뒤의 경우(1을 검사한 후)에도 나올 수 있다고 생각했다. 따라서 나는 n의 모든 생성자를 검사한 다음에 이중에서 최솟값을 결정하였다. 이과정에서 시간이 많이 잡아먹는 것 같아서 생성자들을 저장후 최솟값을 구하는 것이 아니라, 최솟값도 각 상황마다 체크하여 바꿔주었지만, 계속 시간초과 판정이 났다.
내가 놓치는 부분은 그냥 1부터 검사를 해서 최초 생성자가 결정된, 그 생성자가 그냥 모든 생성자들 중 최솟값이 되는거였다.😵
그리고 반복문에서 i의 값을 변경하는 실수도 저질렀다.
소스코드
import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.*;
public class Main2 {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
int n = Integer.parseInt(br.readLine());
int result = 0;
for(int i = 0; i < n; i++) {
int number = i;
int dn = i;
while(number != 0) {
dn += number % 10;
number /= 10;
}
if(dn == n) {
result = i;
break;
}
}
bw.write(String.valueOf(result));
bw.flush();
bw.close();
}
}'Coding Test > 백준' 카테고리의 다른 글
| [트리#2] 백준 11725번: 트리의 부모 찾기 JAVA (0) | 2021.12.27 |
|---|---|
| [트리#1] 백준 1991번: 트리 순회 JAVA (0) | 2021.12.26 |
| [브루트포스#3] 백준 2798번: 블랙잭 JAVA (0) | 2021.11.13 |
| [브루트포스#2] 백준 4673번: 셀프 넘버 JAVA (0) | 2021.11.12 |
| [브루트포스#1] 백준 1065번: 한수 JAVA (0) | 2021.11.12 |





