[Java] 투 포인터(Two Pointers)
배열에 특정 연속된 구간을 처리하는 경우 어떠한 접근 방법이 있을까요?
아래와 같은 문제로 예를 들어봅니다.
문제 예시
- 아래와 같이 자연수로 구성된 수열(배열)이 있습니다.
- 합이 5인 부분 연속 수열의 개수를 구해보세요.
- 시간 제한 : O(N)

답:
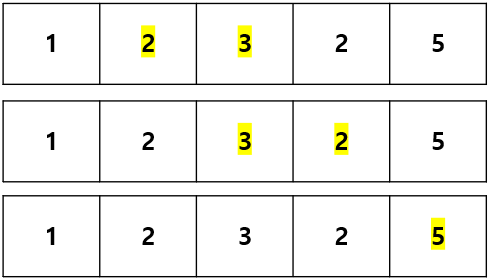
2, 3
3, 2
5
=> 총 3가지
나의 풀이
일단 투 포인터를 모른다고 해서 문제를 풀 수 없는건 아니다. 풀이 방법을 살펴보면, 아래 그림과 같다.
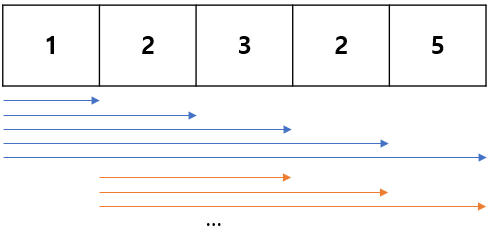
1, 1+2, 1+2+3, 1+2+3+2, 1+2+3+2+5 => 합이 5인지 체크
2, 2+3, 2+3+2, 2+3+2+5 => 합이 5인지 체크
3, 3+2, 3+2+5 => 합이 5인지 체크
2, 2+5 => 합이 5인지 체크
5 => 합이 5인지 체크
답 : 총 3가지
int[] arr = {1, 2, 3, 2, 5};
int sum;
int count = 0;
for (int i = 0; i < arr.length; i++) {
sum = 0;
for (int j = i; j < arr.length; j++) {
sum += arr[j];
if(sum == 5) count++;
}
}
System.out.println(count); //실행결과 : 3자바 소스코드로 작성해보면 위와 같고 시간복잡도가 O(N**2)으로 만약 문제의 시간복잡도가 O(N)으로 제한되어 있을경우 이러한 접근방법은 시간 초과 판정을 받게 될 것이다.
투 포인터(Two Pointers)
Two Pointers 는 1차원 배열에서 두 개의 포인터를 조작하여 원하는 결과를 얻는 알고리즘입니다.
여기서 두 개의 포인터를 사용하여 기존의 방식보다 시간을 개선할 수 있습니다.
즉, 어떤 특정 조건을 만족하는 연속 구간을 처리할 때 O(N) 으로 풀 수 있도록 도와주는 알고리즘
알고리즘의 순서도는 다음과 같다.
- 시작점(start)과 끝점(end)이 첫 번째 원소 인덱스(0)를 가리키도록 한다.
- 현재 부분 합이 M과 같다면, 카운트하고, end를 1 증가시킨다. (M = 5)
- 현재 부분 합이 M보다 작으면, end를 1 증가시킨다.
- 현재 부분 합이 M보다 크다면, start를 1 증가시킨다.
- 모든 경우를 확인할 때까지 1-1번부터 1-3번까지의 과정을 반복한다.
문제에서 합이 5인경우라고 나와있으므로 M = 5이다.
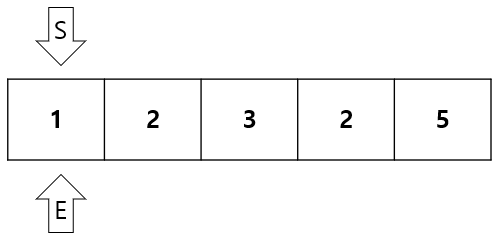
합이 1 < 5 이므로 E(end)를 1증가시킨다.
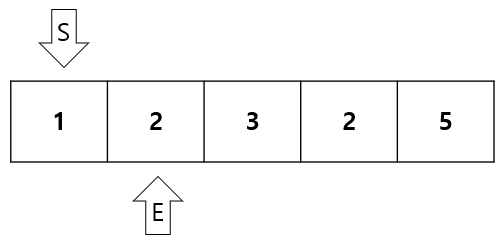
합이 1 + 2 = 3 < 5 이므로 E를 1증가시킨다.
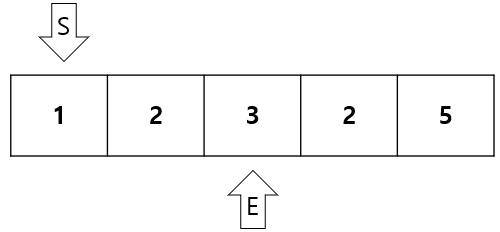
합이 1 + 2 + 3 = 6 > 5 이므로 S(start)를 1증가시킨다.
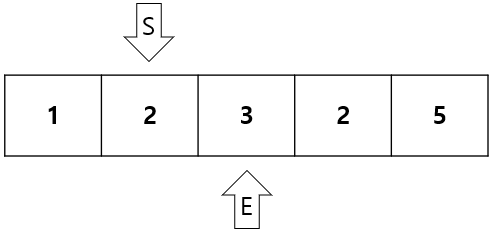
합이 2 + 3 = 5 = 5(M)이므로 count = 1후에 E를 1증가시킨다.
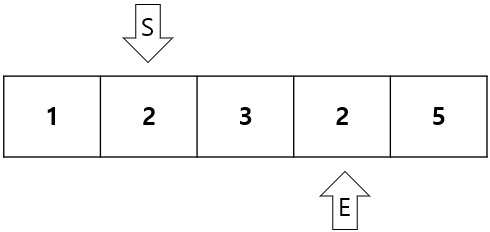
합이 2 + 3 + 2 = 7 >5 이므로 S를 1 증가시킨다.
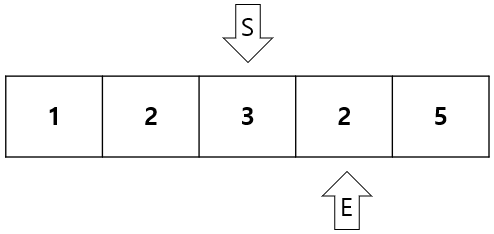
합이 3 + 2 = 5 = 5(M) 이므로 count = 2후에 E를 1증가시킨다.
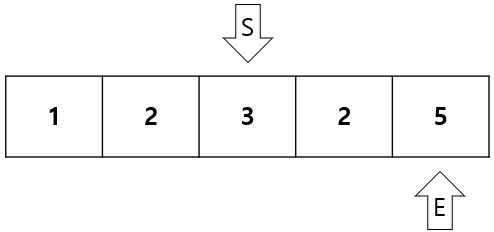
합이 3 + 2 + 5 = 10 > 5 이므로 S를 1증가시킨다.
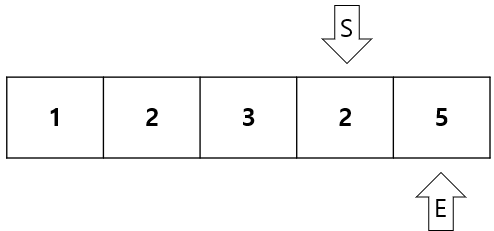
합이 2 + 5 = 7 > 5 이므로 S를 1증가시킨다.
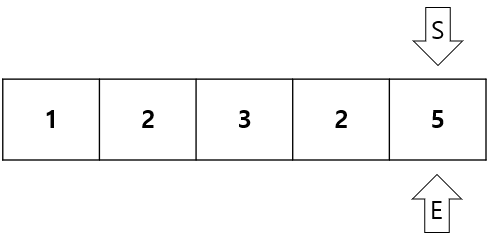
합이 5 = 5(M)이므로 count = 3후에 인덱스의 끝이므로 탐색을 종료한다.
결과 : count = 3이므로 총 3가지
예제코드 1
int[] arr = {1, 2, 3, 2, 5};
int start = 0;
int end = 0;
int sum = arr[0];
int count = 0;
while (true) {
if (sum <= 5) {
end++;
if (end < arr.length) {
sum += arr[end];
}
} else if (sum > 5) {
sum -= arr[start++];
}
if(end >= arr.length) break;
if(sum == 5) count++;
System.out.println("" + start + "/" + end);
}
System.out.println(count);int[] arr = {1, 2, 3, 2, 5};
int start = 0;
int end = 0;
int sum = 0;
int count = 0;
while (true) {
if (sum <= 5) {
if (end < arr.length) {
sum += arr[end];
}
end++;
} else if (sum > 5) {
sum -= arr[start++];
}
if(end > arr.length) break;
if(sum == 5) count++;
System.out.println("" + start + "/" + end);
}
System.out.println(count);위 두개는 같은 접근방식의 코드이지만 sum의 초기값 설정과 end++의 위치 와 end의 범위에 따른 차이가 있다.
위 코드를 둘다 넣은 이유는 투 포인터 구현할 때 알고리즘을 생각하는 것보다 초기값 설정, 반복문이 벗어나는 범위설정(=의 유무), 조건문 조건 설정(=의 유무)등 배열의 인덱스를 넘어가는 실수를 많이하기에 강조 목적으로 접근 방법은 같지만 두가지의 비슷한 코드로 구현해보았다.
예제코드 2
int[] arr = {1, 2, 3, 2, 5};
int end = 0;
int sum = 0;
int count = 0;
for (int start = 0; start < arr.length; start++) {
while (sum < 5 && end < arr.length) {
sum += arr[end++];
}
if(sum == 5) count++;
sum -= arr[start];
}
System.out.println(count);
두가지 스타일로 코드를 짜보았고, 각 상황에 맞게 적절한 구현방법을 선택하면 될 것 같다.
투 포인터 활용
지금까지는 투 포인터가 같은 방향으로 진행하는 예제였지만, 다음과 같은 경우도 활용될 수 있다.
- 포인터 2개가 같은 방향으로 진행해 나아가는 것 (앞에서 시작 or 뒤에서 시작)
- 포인터 2개가 양끝에서 반대로 진행하는 것
- 포인터 하나는 한쪽 방향으로 진행하고, 다른 포인터는 양쪽으로 이동하는 것
'Coding Test > Algorithms' 카테고리의 다른 글
| [Java] 구간 합(Prefix Sum) (0) | 2022.01.18 |
|---|---|
| [Java] 2. 트리(Tree) 구현과 순회 JAVA (0) | 2021.11.20 |
| [Java] 1. 트리의 개념 JAVA (0) | 2021.11.19 |
| [Java] 덱 직접 구현하기 & 라이브러리 사용 JAVA (0) | 2021.11.15 |
| [Java] 큐 직접 구현하기 & 라이브러리 사용 JAVA (0) | 2021.11.15 |





