[Java] 1. 트리의 개념 JAVA
2021. 11. 19. 06:23
1. 트리(Tree)
트리는 노드(Node)들과 이 노드들을 연결하는 링크(link)로 구성되며 계층적 구조를 표현할 때 사용된다.
- 조직도
- 디렉토리 & 서브디렉토리
- 가계도
선형구조(Linear) - 일직선 상
자료를 구성하는 데이터를 순차적으로 나열시킨 형태
ex) 배열, 리스트, 스택. 큐
비선형구조(NonLinear) - 일직선 상에 있지 않음
하나의 자료 뒤에 여러개의 자료가 존재할 수 있는 것을 의미
ex) 트리, 그래프
2. 트리(Tree)의 용어
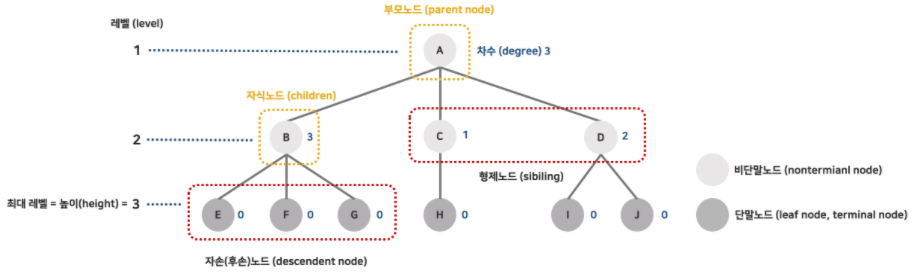
- 노드들 간에는 부모, 형제, 조상, 자손 관계가 존재한다.
- A는 B의 부모 노드(parent node)이며, 반대로 B는 A의 자식 노드(children node)이다.
- B, C, D는 형제 관계(sibling)이다.
- 조상 노드(ancestor node)란 루트 노드에서 임의의 노드까지의 경로를 이루고 있는 노드들이다.
- 후손 노드(descendent node)는 임의의 노드 하위에 연결된 모든 노드들이다.
- 즉, 어떤 노드의 서브 트리에 속하는 모든 노드들은 후손 노드이다.
- 단말 노드(terminal node, leaf node)는 자식 노드가 없는 노드이다.
- 비단말 노드(nonterminal node)는 그 반대이다.
- 노드의 차수(degree)는 어떤 노드가 가지고 있는 자식 노드의 개수이다.
- ex) 루트 노드 A의 경우 자식 노드가 3개이기 때문에 차수도 3이다.
- 단말 노드는 차수가 0인 노드이다.
- 트리의 차수는 트리가 가지고 있는 노드의 차수 중에서 가장 큰 값이다.
- ex) A, B노드의 차수가 3으로 전체 트리의 차수는 3
- 레벨(level)은 트리의 각층에 번호를 매기는 것으로, 루트의 레벨은 1, 한 층씩 내려갈수록 1씩 증가한다.
- ex) A의 레벨은 1, B의 레벨은 2
- 높이(height)는 트리가 가지고 있는 최대 레벨이다.
- ex) 위 그림의 트리의 높이는 3
- 트리들의 집합을 포레스트(forest)라 한다.
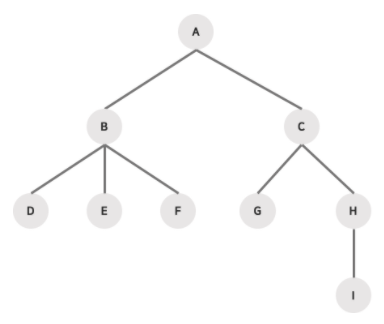
- A는 루트 노드이다.
- B는 D, E, F의 부모 노드이다.
- C는 B의 형제 노드이다.
- D, E, F는 B의 자식 노드이다.
- B의 차수는 3이다.
- 트리의 높이는 4이다.
3. 이진트리
3.1 이진트리 특징
- 모든 노드가 2개의 서브 트리를 가지고 있는 트리를 이진트리(binary tree)라 한다.
- 서브 트리는 공집합일 수 있다.
- 따라서 이진트리의 노드에는 최대 2개까지의 자식 노드가 존재할 수 있고 모든 노드의 차수가 2 이하가 된다.
- 서브 트리 간의 순서가 존재해 왼쪽 서브 트리와 오른쪽 서브 트리로 구별된다.

3.2 이진트리의 정의
- 공집합이거나
- 루트와 왼쪽 서브 트리, 오른쪽 서브 트리로 구성된 노드들의 유한 집합 (이진트리의 서브 트리들은 모두 이진트리여야 한다.)
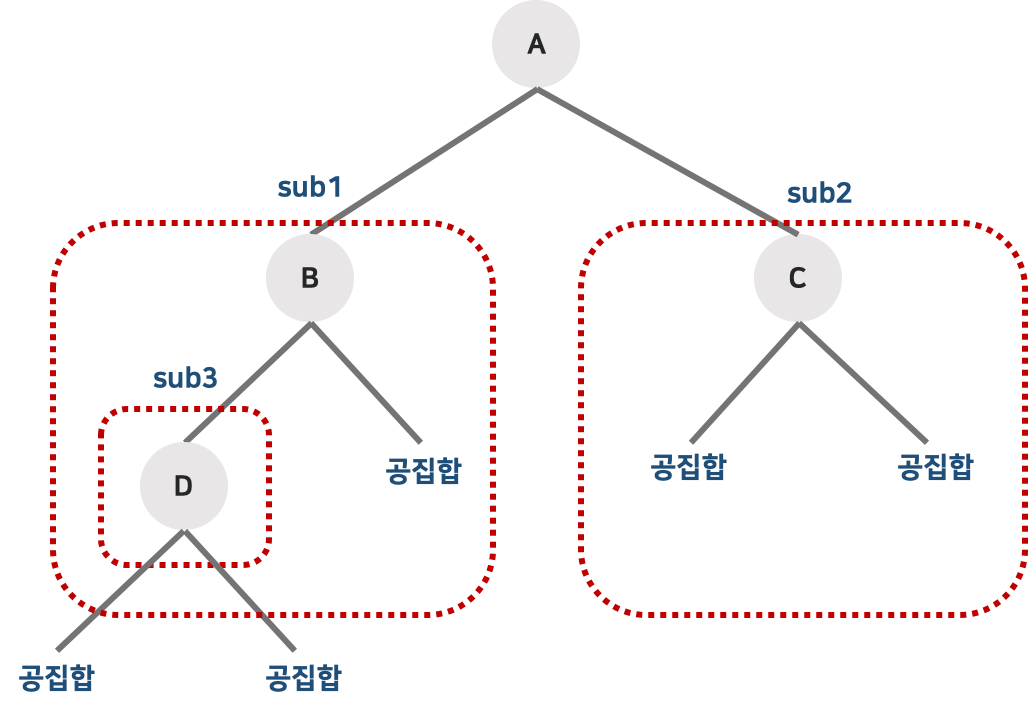
- 위의 그림에서 SUB3은 하나의 노드 D로만 이루어져 있다.
- 노드 D를 SUB3의 루트라고 생각하면 SUB3의 서브 트리는 공집합이다.
- 정의 1에 의해 공집합도 이진트리 이므로 정의 2에 의해 SUB3은 루트와 공집합 서브 트리 2개를 가지는 이진트리이다.
- 같은 식으로 SUB2 역시 루트와 공집합 서브 트리 2개를 가지는 이진트리이다.
- SUB1은 루트 노드 B와 서브 트리 SUB3과 공집합 서브 트리를 가진 이진트리이다.
- 최종적으로 전체 트리는 루트 노드 A와 SUB1, SUB2의 두 개의 서브 트리를 가진 이진트리이다.
3.3 이진트리의 분류
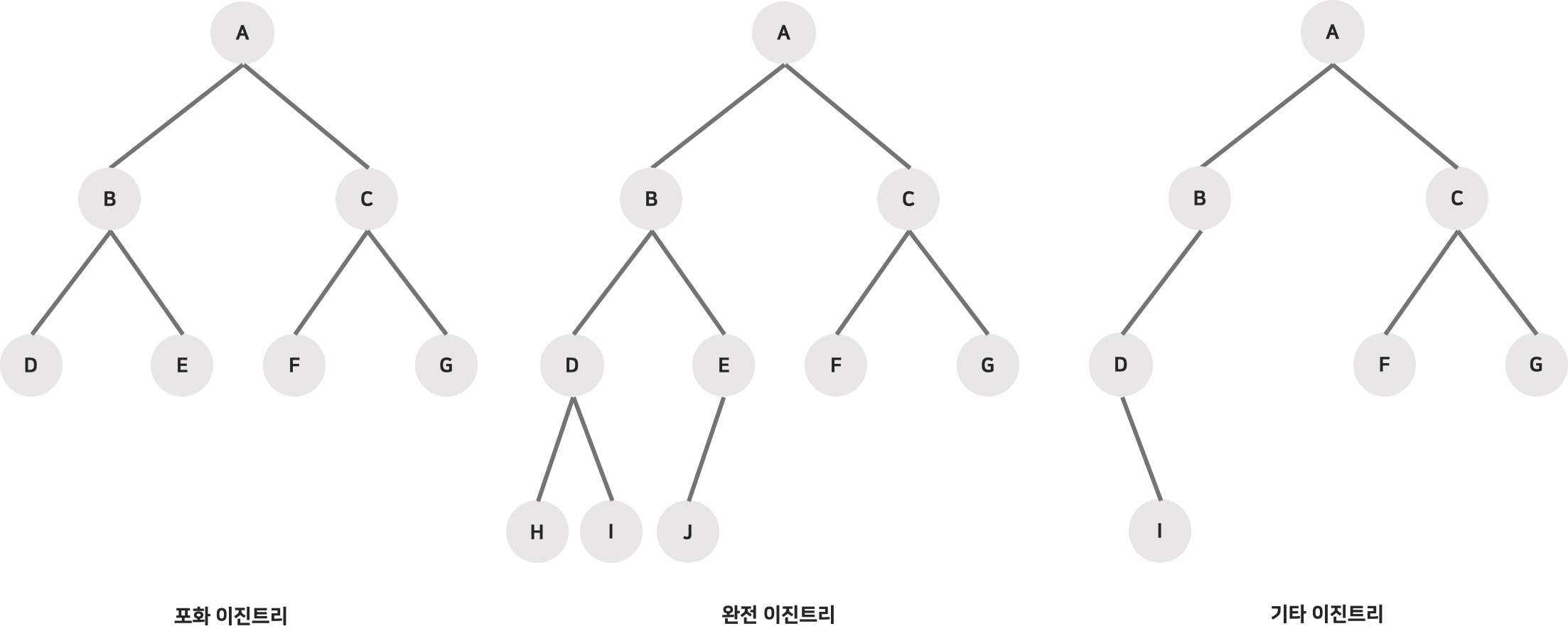
1. 포화 이진트리(full binary tree)
- 각 레벨에 노드가 꽉 차있는 이진트리를 의미
- 높이 k인 이진트리는 정확하게 2^k -1개의 노드를 가진다.
- 각 노드에 번호를 붙일 수 있다.
- 번호는 레벨 단위로 왼쪽에서 오른쪽으로 번호를 붙이면 되고 번호는 항상 일정하다. (A~G -> 1~7)
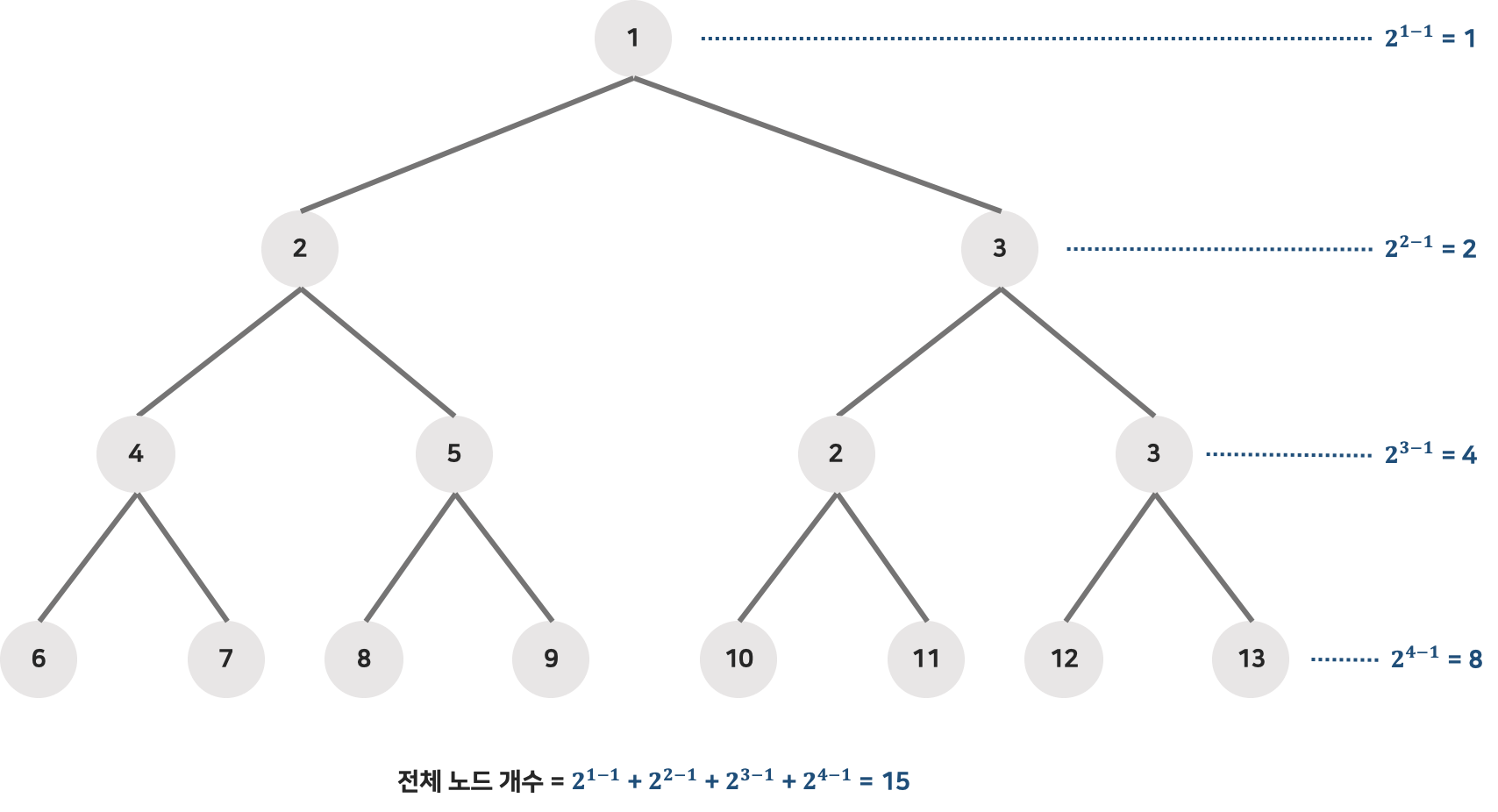
포화이진트리에서의 노드의 개수
2. 완전 이진트리(complete binary tree)
- 높이가 k일 때 레벨 1부터 k-1까지는 노드가 모두 채워져 있고 마지막 레벨 k에서는 왼쪽부터 오른쪽으로 순서대로 노드가 채워져 있다.
- 마지막 레벨에서는 노드가 꽉 차 있지 않아도 되지만 중간에 빈 곳이 있어서는 안 된다.
- 따라서 포화 이진트리는 항상 완전 이진트리이지만 그 역은 성립 안됨
- 번호를 붙일 수 있음
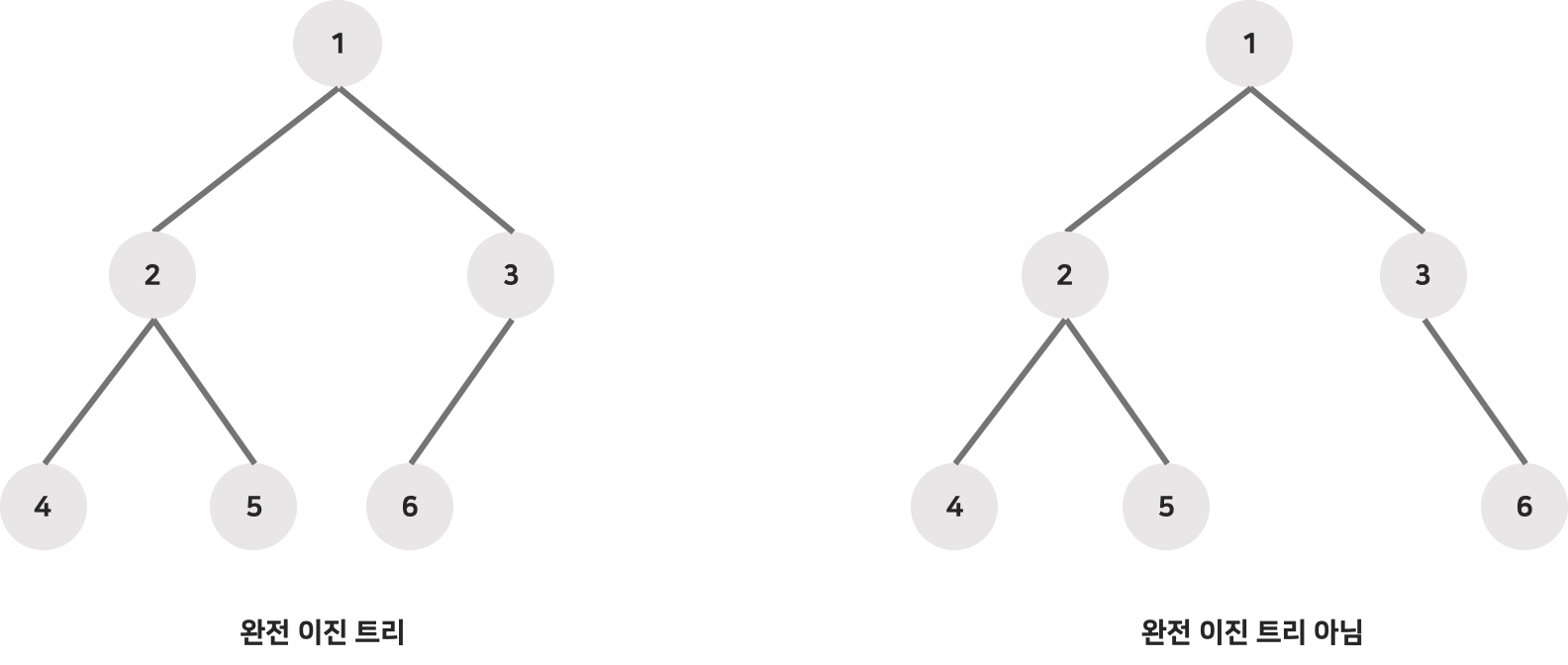
4. 이진트리 표현법
- 1차원 배열 이용
- 2차원 배열 이용
- 노드(클래스) 이용
구현방법은 다음 포스터에서..
[Java] 2. 트리(Tree) 구현과 순회 JAVA
트리를 구현하는 방법은 크게 3가지가 있다. 1차원 배열을 이용 2차원 배열을 이용 노드(클래스)를 이용 트리를 구현하는 방법 중 배열을 이용한 방법은 배열의 크기가 정해져있기 때문에 한계
heesangstudynote.tistory.com
출처 : C언어로 쉽게 풀어쓴 자료구조(개정 3판) - 생능 출판 - 8장 트리
'Coding Test > Algorithms' 카테고리의 다른 글
| [Java] 투 포인터(Two Pointers) (0) | 2022.01.18 |
|---|---|
| [Java] 2. 트리(Tree) 구현과 순회 JAVA (0) | 2021.11.20 |
| [Java] 덱 직접 구현하기 & 라이브러리 사용 JAVA (0) | 2021.11.15 |
| [Java] 큐 직접 구현하기 & 라이브러리 사용 JAVA (0) | 2021.11.15 |
| [Java] 스택 직접 구현하기 & 라이브러리 사용 JAVA (0) | 2021.11.15 |





